Quintic Automatic Tracking

Q4E Case Study 9 – Quintic Validation study of Automatic Tracking Accuracy

Objective

• To analyse the accuracy and reliability of the new Quintic Automatic Tracking function. As the bicycle wheel is a constant size throughout the recording, we can assume that length b and angle ACB are invariant (this should remain constant). Therefore if the automatic tracking is accurate length ‘b’ should remain constant.

  
  Figure 1

Method

4 reflective markers where placed on a bicycle wheel, 1 in the middle, and 3 around the outer rim. Video footage was then recorded using a Redlake camcorder at 250fps and captured using Quintic Biomechanics Video Analysis Software. The videos were later calibrated horizontally and vertically by measuring the distance between the markers. The captured clips were then automatically digitised, and butterworth filters were applied to the data, to smooth any errors. Quintic software automatically selects the correct filter value, to remove any residual noise from the data. Both the X and Y co-ordinates for each marker are smoothed individually, to reduce the likelihood over smoothing or under smoothing the data.

Analysis : Calculating length ‘b’

Figure 2

By exporting the absolute data from Quintic into excel Pythagoras theory can be used to calculate ‘b’. When using the absolute data from Quintic all of the exported data is calculated from (0.0) which is in the bottom left corner of the video. If the relative data is being used all of the data is calculated from (0.0) which is the position of that marker at frame 0.

In order to calculate b the other sides of the right-angled triangle must first be calculated. To calculate side ‘c’ of the triangle, the vertical displacements of both marker A and C are used. Ay – Cy = c. To calculate side ‘a’ the horizontal displacements of markers A and C are used. Ax – Cx = a.

Figure 3

Pythagoras can now be used to calculate length ‘b’.

For FRAME 1

C			A
Frame	Horizontal	Vertical	Frame	Horizontal	Vertical	a Ay-Cy	c Ax-Cx		b
Number	Distance	Distance	Number	Distance	Distance
1	0.65	0.21	1	0.52	0.45	0.123	-0.593	0.37	0.606
2	0.65	0.21	2	0.52	0.45	0.128	-0.592	0.37	0.606
3	0.65	0.21	3	0.52	0.45	0.134	-0.591	0.37	0.606
4	0.66	0.21	4	0.52	0.44	0.140	-0.589	0.37	0.606
5	0.66	0.21	5	0.51	0.44	0.147	-0.588	0.37	0.606

Average = 0.606m
Standard Deviation ± 0.001m

Graph 1: Length ‘b’ during one complete revolution of the wheel

Figure 4

Graph 1 shows the diameter of the wheel throughout the experiment. The diameter was calculated using the same process as above for every frame (please see attached excel spreadsheet). On average the diameter of the wheel measured 0.606m with a standard deviation value of ± 0.001m. Three areas have been highlighted on the graph (red circle) as well as in figure 4, where the wheel diameter changes suddenly; this is due to one of the reflective markers been automatically tracked by the Quintic software, travelling behind the brake pad or frame of the bike. While the marker is behind the brake pad or frame it cannot be recognised/tracked by the software and is therefore interpolated until it is visible once again. This interpolation of the markers causes slight errors to occur in the final data but nothing of any significant value.

Calculating Angle ACB

Figure 5

As well as length ‘b’ being an invariant so is angle ACB, therefore this angle should remain constant throughout the complete revolution of the wheel if the automatic tracking is accurate.

Calculating length ‘a’ : By using the same procedure to calculate length ‘b’ we can now calculate length a,

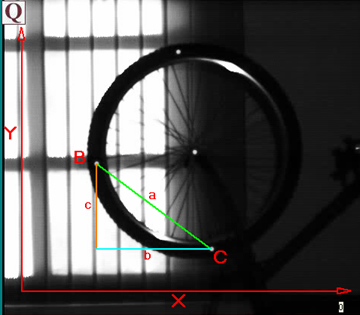
Figure 6

In order to calculate ‘a’ the other sides of the triangle must first be calculated. To calculate side ‘c’ of the triangle, the vertical displacements of both marker B and C are used. By – Cy = c. To calculate side ‘b’ the horizontal displacements of markers A and C are used. Bx – Cx = a

For Frame 1 : Pythagoras Theory states that:

Average = 0.435m
Standard Deviation ± 0.030m

Calculating length c : We can now use the same procedure again to calculate length ‘c’

Figure 7

For Frame 1 : Pythagoras Theory states that:

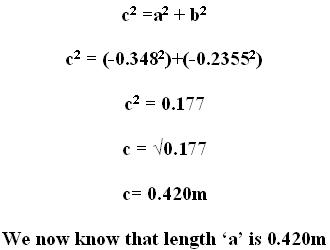
Average = 0.420m
Standard Deviation ± 0.001m

Calculating Angle ACB

To calculate angle ACB we can use the following Cosine equation, as we know the lengths of all the respective sides.

For frame 1

Average = 43.73°
Standard Deviation ± 0.095°

Graph 2: Angle ACB throughout one complete revolution

Figure 8

Graph 2 shows the angle ACB throughout the experiment. The angle was calculated using the same process as above for every frame (please see attached excel spreadsheet). On average the angle of ACB was calculated at 43.73° with a standard deviation value of ± 0. 095°. Four areas have been highlighted on the graph (red circle) and in figure 8 the angle changes suddenly; this is due to one of the reflective markers been automatically tracked by the Quintic software, travelling behind the brake pad or frame of the bike. While the marker is behind the brake pad or frame it cannot be recognised/tracked by the software and is therefore interpolated until it is visible once again. This interpolation of the markers causes slight errors to occur in the final data but nothing of any significant value.

Conculsion
The actual physical distance of the wheel was measured at a length of 0.608 metres. On average the diameter of the wheel measured using the above procedure was 0.606 metres with a standard deviation value of ± 0.001. The minor difference in diameter can be due to the errors caused during the interpolation or due to minor errors during the calibration. However, it can be seen from the above study that the accuracy of the Quintic software when measuring the distance of the wheel during one complete cycle (360°) was within 2mm tolerance.

Downloads

Written Case Study	Excel Data Spreadsheet	Video 1
~0.8 MB	~0.3 MB	Wheel ~1.8 MB