Q4E Case Study 14 – Moment of Inertia
Proposed Subject usage:
Mathematics / Physics (A/AS level), Sports Science (Degree Yr 1/2)
Introduction
Moment of inertia of an object is an indication of the level of force that has to be applied in order to set the object, or keep the object, in motion about a defined axis of rotation. Moment of inertia, which is a derivative of Newton’s second law, is sometimes referred to as the second moment of mass and can be calculated using the equation:
I = mr²
Where:
I = Moment of Inertia (kg m²)
m = Mass (kg)
r = Radius (m) (shortest distance from the axis of rotation to the particle)
Higher moments of inertia indicate that more force has to be applied in order to cause a rotation whereas lower moments of inertia means that only low forces are necessary. Masses that are further away form the axis of rotation have the greatest moment of inertia.
Angular momentum of an object, rotating about an axis, is a measure of the amount of rotation of that object when no external torques are acting upon it, with torque being defined as the moment of force and is a measure of how much force is needed to cause the rotation of an object. Angular momentum is a conserved quantity, which means that it stays constant providing no external torques act upon it, and is the product of moment of inertia multiplied by angular velocity. When the body has an increased radius, i.e. during the initial and final phase of a dive, moment of inertia is large and angular velocity is small. While in the pike position the body decreases in radius as each segment moves closer to the axis of rotation, resulting in angular velocity increasing and a decrease of moment of inertia. Thus, during a dive, angular momentum is constant meaning that moment of inertia is inversely proportional to angular velocity.
Objectives
- To find and analyse the Moment of Inertia of a forward and backward pike dive.
- To compare the differences in the Moments of Inertia of both dives.
Methods
- The videos have been digitised and calibrated using the
Quintic
- software.
- A butterworth filter was used to smooth the data.
- Data has been exported to an excel file where it was used to calculate the moment of inertia. Graphs were prepared using this information.
- Still images have been captured.
Functions of the Quintic Software used:
- Multi-Point Digitisation Module
- Butterworth Filter
- Calibration
- Interactive Graph and Data displays
- Export Data
- Multi-Image Capture
Results
Moments of Inertia were found for a backward and a forward pike dive by calculating the sum of the inertias for each segment of the body. Both dives were performed by the same diver yet the moments of inertia are different due to the distance of each segment from the axis of rotation i.e. the hip, being different for both dives and the differences in the angular velocity throughout the dives.
 |
Divers always aim to complete the required number of somersaults and/or twists as quickly as possible leaving more time to prepare for entry into the water. In order to do this they have to increase their angular velocity, consequently reducing their moment of inertia. This is done by changing their body configuration so as to decrease the distance between the centre of mass of each body segment and the axis of rotation, thus a tighter pike position gives the diver a smaller moment of inertia and greater angular velocity. Once the diver leaves the board, there is no torque acting on the body. This means that angular momentum is conserved when no external torque acts on it, thus when the moment of inertia decreases angular velocity increases and vice versa.
The dive is divided into 3 phases. The first phase is from when the diver leaves the board until entering the full pike position. Phase 2 is the execution of the somersaults in the pike position and the final phase is the release from the pike position and preparation for entry into the water. In phase 1, once the diver leaves the board there is no external torque acting on him, thus angular momentum is conserved and remains so throughout the dive. When the diver first leaves the board, moment of inertia is high due the limbs i.e. the arms being outstretched and further away from the axis of rotation. Towards the end of phase 1, the diver is assuming the pike position meaning that all body segments are pulled as close as possible to the axis of rotation thus decreasing the moment of inertia and increasing the angular velocity. Moment of inertia in the second phase varies in accordance with the angular velocity so as to conserve angular momentum. By the third phase the moment of inertia increases as the diver prepares to enter the water and releases from the pike position. This is because the arms are stretched over the head and are thus further away from the axis of rotation, similar to the initial position. The increased moment of inertia slows down the angular velocity and allows the diver to prepare for entry into the water in as straight a line as possible so as to produce minimum splash.
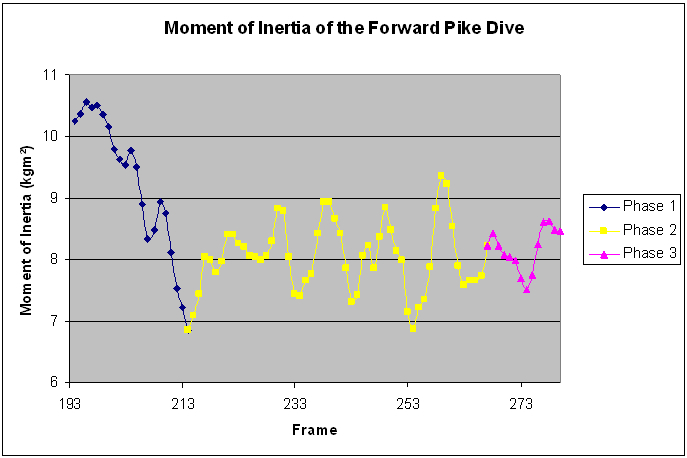
Graph 1: Moment of Inertia during a Forward Pike Dive
Graph 1 shows the calculated moment of inertia of the diver during a forward pike dive. The graph has been divided into the 3 different phases. In phase 1, as the diver is leaving the board, the inertia is 10.25kgm². After a slight increase, the inertia decreases rapidly as the diver assumes the pike position. At the end of this phase, moment of inertia is 6.86kgm². The diver is in the full pike position now and is starting the somersaults. During the dive, inertia is constantly varying between 6.86 – 9.36 kgm²; this is due to the varying angular velocity during each somersault. As the angular velocity increases, moment of inertia decreases and vice versa hence keeping angular momentum constant throughout the dive. In the final phase, the inertia initially decreases but as the divers straightens up; preparing to enter the water the moment of inertia begins to rise.
 |
Figure 1: Forward Pike
 |
Graph 2: Moment of Inertia of a Backward Pike Dive
Graph 2 shows the moment of inertia for the backward pike dive. The graph is again divided into the 3 different phases. Initially, in phase 1, the moment of inertia is 11.41kgm². Once the diver has left the board, the moment of inertia decreases and continues to decrease until the diver assumes the pike position at the end of phase 1. During the second phase, the moment of inertia fluctuates in accordance with the decreasing angular velocity, keeping angular momentum constant. At frame 222, the diver is starting to prepare for his entry into water and thus begins to release from the pike position. As he does so, the moment of inertia increases and continues to increase as the diver stretches out fully in order to enter the water in a straight line.
 |
Figure 2: Backward Pike
 |
Graph 3: Comparison of Moments of Inertia
Graph 3 shows a comparison between the moments of inertia for both the forward and backward pike dives. The dives were compared from the frame of last contact with the board until the diver enters the water. The moment of inertia for the forward pike is more variable throughout the dive, yet both dives still follow a similar pattern. As the diver leaves the board moment of inertia decreases for both dives. The backward pike dive takes a bit longer to decrease fully due it taking slightly longer to reach the pike position during a backward dive. However, the backward pike dive decreases to a lower moment of inertia meaning that the angular velocity is greater and that the diver is in a tighter pike position during the backward pike. At the end of the dive, inertia increases as the angular velocity decreases. The backward pike dive has a greater increase in the inertia due to the decrease in the angular velocity. As the forward pike dive had a slower angular velocity, there is less of an increase in inertia as the diver enters the water.
Conclusion
Moment of inertia is a calculation of the required force to rotate an object. The value can be manipulated to either increase or decrease the inertia. In sports such as ice skating, diving and gymnastics athletes are constantly changing their body configuration. By increasing the radius from the axis of rotation, the moment of inertia increases thus slowing down the speed of rotation. Alternatively, if an athlete wants to increases the speed of rotation, then they must decrease the radius by bringing the segments of the body closer to the axis of rotation thus decreasing the radius and moment of inertia.
Downloads
|
Written Case Study
|
Video avi. files
|
|