Q4E Case Study 19 – Simple Harmonic Motion
Proposed Subject usage:
Mathematics / Physics (A/AS level), Sports Science (Degree Yr 1/2)
Introduction
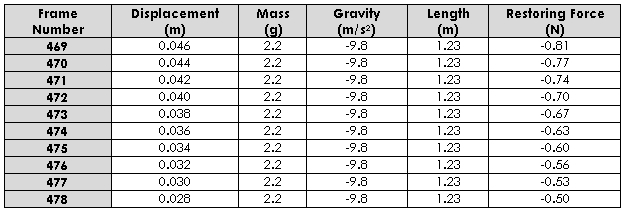
In classical mechanics a harmonic oscillator is a system, which when displaced from its equilibrium position, experiences a restoring force proportional to its displacement. This is described by Hooke’s Law and represented by the equation below;
SHM : equation 1 Hooke’s Law
Where;
F is the restoring force
x represents the displacement from the equilibrium
k is a positive constant
If F is the only force acting on a system, the system is called a simple harmonic oscillator and it is said to undergo simple harmonic motion (SHM). SHM is a motion that is neither driven nor damped (i.e. no friction to slow the pendulum down); the motion is periodic as it repeats itself at standard intervals in a specific manner. It can also be described as the repetitive back-and-forth movement through a central or equilibrium position in which the maximum displacement on one side is equal to the maximum displacement on the other. SHM is characterized by its amplitude (maximum distance that the mass is displaced from its equilibrium), its period (time for a single oscillation), its frequency (the number of cycles per unit time) and its phase (determines the starting point on the sine wave). The period and frequency are constants determined by the overall system, while the amplitude and phase are determined by the initial conditions of that system.