|
Q4E Case Study 24 – Dynamics of Vertical Jump Dr Stelios G. Psycharakis
There is a variety of different vertical jumps that an athlete can perform, depending on: position (static or following a run-up); take-off (from one foot or both feet); arm movement (with or without an arm-swing), and; legs movement (counter-movement or squat). The purpose of the present study was to compare two types of static jump with take-off from both feet: a counter-movement jump with an arm-swing (CMJ-AS) and a squat jump with no arm swing (SJ-NAS). Methodology One male participant (age: 29.8 years, height: 178.5cm, body mass: 79.3kg) who was an active recreational athlete performed a standardised 10-min warm-up before participating in this study. The warm-up included elements of static and dynamic stretching, a light jog and some jumping drills. Following the warm-up, the technique of each jump was explained to the participant and he was given practice trials for familiarisation. A series of 12 jumps was then performed (6 CMJ-AS and 6 SJ-NAS) in a randomised order, and the jump with the highest peak height from each type was chosen for further analysis. For the SJ-NAS the participant was instructed to adopt a squatting position, with the arms crossed over his chest. On the operator’s signal the participant attempted a maximal vertical jump. The push off phase of the SJ-NAS had to be initiated with an upwards movement of the body. Thus, any jumps that were initiated with downward movement (i.e. counter-movement) of the body were discarded and had to be repeated. Figure 1 shows a series of still images of four key events of the SJ-NAS jumps: start (which was also the position of maximum knee flexion), take off, peak height and landing. For the CMJ-AS the participant had to start from a standing position, with the legs straight and the arms straight and parallel to the ground. He then had to bend the legs and integrate a full arm swing while jumping for maximal height. Figure 2 shows a series of still images of four key events of the CMJ-AS jumps: start, maximum knee flexion, take off and peak height.
|

Figure 1: Four key events of the SJ-NAS jumps performed: 1) start (position of maximum knee flexion), 2) take off, 3) peak height and 4) landing. (Figure 1 was prepared through the Report and Photo Sequence options of the Quintic Biomechanics software).

Figure 2: Four key events of the SJ-AS jumps performed: 1) start, 2) position of maximum knee flexion, 3) take off and 4) peak height. (Figure 2 was prepared through the Report and Photo Sequence options of the Quintic Biomechanics software).
Quintic spherical markers of a 19 mm diameter were placed on the following anatomical landmarks of the right side of the participant: temple, shoulder (humeral head), elbow (ulnohumeral joint), wrist (radiocarpal joint), hip (greater trochanter), knee (lateral epicondyle), and lateral ankle. Two Quintic spherical markers were fixed on the ground, one metre apart and at the same plane of movement as that of the subject, for subsequent calibration. A Casio (EX-FH25) video camera was placed on a tripod 10m away from the subject at a height of 1.5 m. The side view of each jump was recorded at a rate of 120 Hz with a shutter speed of 1/160 sec. The Quintic Biomechanics software was used for data processing and the following variables were calculated: peak height of the jumps (cm), take off velocity (m∙s-1); peak angular velocity of the knee (degrees/sec); angle of maximum knee flexion (degrees). The following functions of the Quintic Biomechanics software were used during the processing:
-
Single Camera System: Premier Capture Editor (for video trimming)
-
Single Camera System: Premier Capture Filter (for video rotation)
-
Report: Photo Sequence (Still image photo capture of sequence)
-
Video file calibration
-
Automatic digitisation of a new trace
-
Manual digitisation of a new trace
-
Data smoothing of trace
-
Digitisation analysis for linear variables
-
Digitisation analysis for angular variables
-
Interactive graph and data displays
-
Export data
Results:
Table 1 shows the results from the processing of the variables of interest for the best two jumps of each type. The peak height reached with the CM-AS was 14.5 cm (40.2%) higher than the SJ-NAS (Figure 3). In the former jump the participant managed to produce a velocity at take off that was 0.61 m∙s-1 (25.8%) higher than the take off velocity of the SJ-NAS. Interestingly, in both jumps the participant seemed to achieve his maximum vertical velocity of the push off phase (3.12 m∙s-1 and 2.60 m∙s-1, for the CM-AS and the SJ-NAS, respectively) around 0.02 – 0.03 sec before the take off. The participant flexed his knees in the push off phase much more during the CM-AS than the SJ-NAS jump, with the difference being 42.7° (60.7%). Finally, peak angular velocities reached during the push off phases of the two jumps were similar, with the difference being just 29.8 degrees/sec (3.6%).
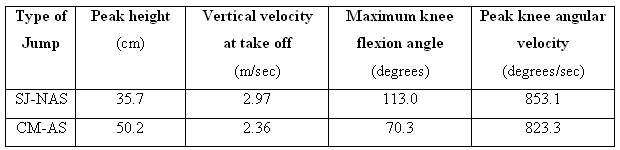
Table 1: Comparison between a counter-movement jump with an arm-swing (CM-AS) and a squat jump with no arm swing (SJ-NAS)

Figure 3. Overlay images for the best two jumps of each type. The peak height reached with the CM-AS was 14.5cm (40.2%) (left hand image) higher than the SJ-NAS (right hand image).
Conclusion:
The better performance achieved with the CM-AS jump can be primarily attributed to two reasons: the counter-movement of the legs and the arm swing. The counter movement of the legs stimulates a stretch-shortening effect of the muscles. At the downward part of the push off phase of this jump, the hip, knee and ankle extensors are increasing in length (stretching) while resisting the flexion of the joints, before they start decreasing in length (shortening) at the upward part of the push off phase. As explained by Enoka (1994), the advantage of this strategy is that muscles can perform more positive work if they are actively stretched before they are allowed to shorten, as they can store and utilise elastic energy. Thus, a greater amount of work is done during the concentric contraction that would be done if the muscles simply performed a concentric contraction only, as was the case in the SJ-NAS. Grimshaw et al. (2007) stated that the counter movement action seems to add about 10% to the peak height achieved during a jump.
One could perhaps argue that the SJ-NAS also includes a counter-movement motion, as the participant had to get to a squat position before the start of the jump. However, the participant had to maintain this position for a minimum of 5 seconds before he was instructed by the operator to perform the jump. On the contrary, the downward and upward movements for the CMJ-AS were performed continuously, without any delay between the stretch and shortening cycles. Given that the ability of the muscles to store and utilise elastic energy decreases when the delay between the stretch and shortening cycles increases, the long pause between these two cycles during the SJ-NAS suggests that much of the ability of the muscles to utilise the elastic energy and perform more positive work had been lost.
The arm swing used in the CM-AS was the other main contributor to the better performance achieved in this jump. Grimshaw et al. (2007) stated that the mechanism through which the arm swing contributes to jumping performance is believed to be related to both a direct contribution to the momentum of the centre of mass (upward and forward movement of the arms will contribute to upward and forward movement of the centre of mass) and to the creation of larger ground reaction forces. These authors stated that an arm swing has been shown to add 10%-20% in the distance achieved in a jump.
Overall, the values recorded for the jumps performed in the present study were within the range of those reported in the literature for participants of similar level, and the differences found between the two jumps can be therefore considered typical of such jumps. For example, McLellan et al. (2011) reported peak CM-AS jump heights of 55 ± 10 cm for a group of active recreational athletes. For SJ-NAS jumps, Walshet al. (2007) reported peak heights of 30 ± 6 cm for a group of recreational athletes, while Requena et al. (2009) reported peak heights of 32 ± 5 cm for a group of competitive soccer players. Walsh et al. (2007) also reported a mean improvement of 30% in the peak jump height between SJ-NAS and CM-AS. The take-off velocities found in the latter study were 2.40 m∙s-1 and 2.73 m∙s-1 for the SJ-NAS and CM-AS jump, respectively. Interestingly, the participant in the present study reached angles of maximum knee flexion of 70.3° CM-AS and 113° for the SJ-NAS jump. Although angles of maximum knee flexion are not always calculated in vertical jump studies, it has been reported that an angle of around 90° would normally produce a higher peak height (Salles et al., 2011; Moran and Wallace, 2007). This suggests that the participant of the present study could improve the peak height of his jumps further if he modifies the movement so that a maximum knee flexion angle closer to 90° is achieved.
References:
Enoka, RM, 1994. The Motor System. In: Neuromechanical Basis of Kinesiology (2nd Edition). Human Kinetics Publishers. Leeds, UK. Pp. 231-269.
Grimshaw P, Lees A, Fowler N and Burden A, 2007. Biomechanics of Jumping. In: Instant Notes for Sport and Exercise Biomechanics. Taylor and Francis Group, Abingdon, UK. Pp. 261-266.
Kale M, Asçi A, Bayrak C and Açikada C, 2009. Journal of Strength and Conditioning Research. 23(8): 2272-2279.
McLellan CP, Lovell DI and Gass GC, 2011. The role of rate of force development on vertical jump performance. Journal of Strength and Conditioning Research. 25(2): 379-385.
Moran KA and Wallace ES, 2007. Eccentric loading and range of knee joint motion effects on performance enhancement in vertical jumping. Human Movement Science. 26: 824-840.
Requena B, Gonzalez Badilo JJ, De Villarreal ESS, Ereline J, Garcia I, Garpeyeva H and Paasuke M, 2009. Functional performance, maximal strength, and power characteristics in isometric and dynamic actions of lower extremities in soccer players. Journal of Strength and Conditioning Research. 23(5): 1391-1401.
Salles AS, Baltzopoulos V and Rittweger J, 2011. Differential effects of countermovement magnitude and volitional effort on vertical jumping.European Journal of Applied Physiology. 111: 441-448.
Vizcaya FJ, Viana O, Del Olmo MF and Acero RM, 2009. Could the deep squat jump predict weightlifting performance? Journal of Strength andConditioning Research. 23(3): 729-734.
Walsh MS, Bohm H, Butterfield MM and Santhosam J, 2007. Gender bias in the effects of arms and countermovement on jumping performance. Journal of Strength and Conditioning Research. 21(2): 362-366.
Downloads
