Q4E Case Study 26 – Position of the Non-Kicking Foot in Football Penalty Kicks
|
Proposed subject useage
|
||
|
Sports Science / Mathematics / Physics (A/AS level) / Sports Science (Degree Yr 1/2) |
Q4E Case Study 26 – Position of the Non-Kicking Foot in Football Penalty Kicks
|
Proposed subject useage
|
||
|
Sports Science / Mathematics / Physics (A/AS level) / Sports Science (Degree Yr 1/2) |
Introduction
This case study aims to assess the different variables which affect penalty shots in football, with the ultimate intention of being able to educate keepers to be able to more consistently predict where within the goal the shot will end up. Penalty kicks can win or lose a game of football, and so by giving the keeper that extra knowledge to ‘know’ where the ball is going could be extremely advantageous in competitive situations.
Research suggests that there are certain cues to look out for. Lees and Owens (2011) completed a study on the visual cues associated with penalty shots, and concluded that the best cue goal keepers can use is the orientation of the support leg. They however suggest that it is this orientation before the foot is planted on the ground. This case study aims to look at any correlation just prior to ball contact, when the foot is planted and this is something Franks and Hanvey (1997) investigated, concluding that orientation of the non-kicking foot is the optimal source of information available prior to ball contact.
With the use of video analysis equipment in the form of Quintic Biomechanics v21, and data analysis programs, a number of different variables were considered to see if the position of the plant foot just prior to ball contact could be used as an indication of the path of the ball.
Methods
Procedure
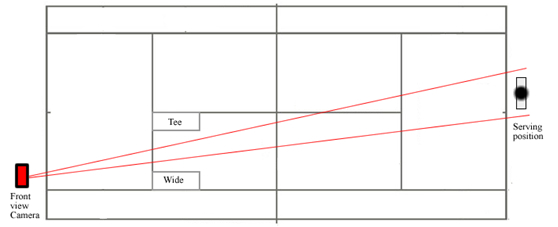
100 penalty kicks were taken by four University football players (25 each) against a goalkeeper on a standard grass pitch. A full size goal was used (7.32 m x 2.44 m) and was marked with tape halfway down the sides and at 1 m intervals along the crossbar to help identify areas of the goal. Two Quintic High Speed GigE cameras were set up (as shown in Figure 1), one back view and one side view, running at 100 fps and 80 fps respectively. The back view camera was used to quantify angle of the plant foot as well as the position of the ball where it crosses the goal line, and the side view camera to quantify the launch angle of the ball and the position of the plant foot in relation to the ball. All data was collected (and subsequently analysed) using Quintic Biomechanics v21 software. The space was calibrated for both the back view and side view cameras by calibrating the diameter of the football as 22cm for calculations where the action was at the penalty spot, and for when calculating the ball position as it crossed the goal line, a calibration frame was used (dimensions: 2.002 m x 1.002 m from the centre of the white corner markers on the frame), positioned on the goal line.
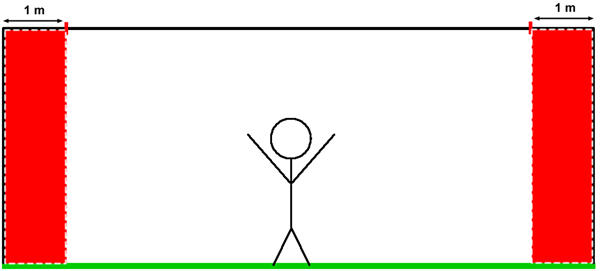
Each striker was asked to take ten shots against the goalkeeper before rotating with the other players until each had taken a total of 25 penalties (whether successful or not). The strikers were instructed to strike the ball so as it entered the goal within 1 m of either outside post (see Figure 2), using kicks of varying speeds. All shots were counted regardless of whether or not this was achieved.
Data Analysis
As previously mentioned, all video analysis was carried out in the Quintic Biomechanics v21 software. The analysis was split into two sections, that from the back view camera, and that from the side view camera.
Back View (BV) Camera: Each video was calibrated using the procedure previously specified. Each penalty was scrolled to the frame where initial ball contact is made. At this frame, the position of the plant foot was classified in relation to the following criteria (see Figure 3 below).
This angle was noted / whether the foot was pointed left (<-5°), down the middle (-5°<0>5°) or right (>5°).
Additionally, the position of the ball within the mouth of the goal where it crosses the goal line (or if in the case of the keeper saving the ball, the position where the keeper makes initial contact with the ball). A screenshot of this frame was taken, along with an image of the ball position for all penalties. Using the ruler tool under the Digitisation tab of Quintic Biomechanics v21, this position can then be calculated in terms of a x and y distance, in this case relative to the top left hand corner of the goal (i.e. 0 m, 0 m). (See Figure 4.)

Finally the distance the big toe of the plant foot was away from the centre of the ball was calculated by finding the distance between the pixel value of the centre of the ball, and the pixel value corresponding to the big toe. (See Figure 5.)

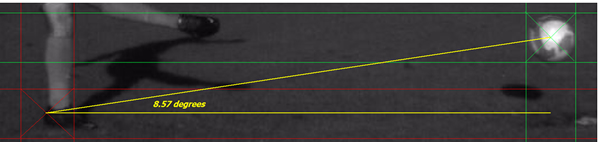
Side View (SV) Camera: Each video was calibrated using the procedure previously specified. The launch angle of the ball was calculated by identifying the initial position of the centre of the ball and its position in the frame before the ball went out of shot. The angle to the horizontal function in Quintic Biomechanics v21 was used to quantify this angle. (See Figure 6.)
In addition to calculating how far the plant foot was away from the ball from the back view camera, this was also down from the side view to look whether the foot (measured from the big toe) was in front / behind relative to the centre of the ball. (See Figure 7.)

It is important to note that the effect of any parallax error was considered, but it was concluded that it would be so insignificant and small that it was ignored.
In terms of statistical analysis, this was completed in the program PASW Statistics 18 (SPSS) and in Microsoft Excel.
Results
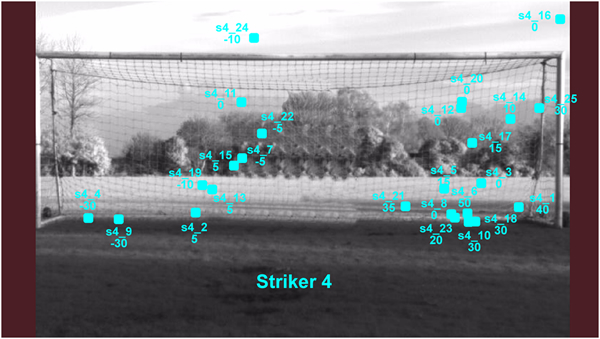
The results of the data collection for each striker can be found in the following respective tables (Table 1 – 4). Additionally, a diagram of where each shot crossed the line for each striker is displayed in Figures 8 – 11 respectively.
(N.B. Although 100 kicks were taken by the strikers, due to missing videos and data, the results are only displayed for a total of 82 kicks.)
Table 1: Striker 1
|
Shot |
Foot Angle |
Launch Angle |
Distance Foot Away From Ball (BV) |
Distance Toe in Front of Ball (SV) |
Position of ball (m) |
|
|
(position) |
(°) |
(m) |
(m) |
x |
y |
|
|
s1_11 |
Right |
7.69 |
0.25 |
0.23 |
5.83 |
1.36 |
|
s1_12 |
Right |
2.76 |
0.29 |
0.21 |
0.69 |
2.32 |
|
s1_13 |
Left |
19.56 |
0.32 |
0.20 |
1.00 |
Over |
|
s1_14 |
Right |
12.50 |
0.31 |
0.21 |
6.14 |
Over |
|
s1_15 |
Right |
8.10 |
0.21 |
0.20 |
6.88 |
1.20 |
|
s1_16 |
Right |
10.23 |
0.19 |
0.19 |
6.74 |
1.17 |
|
s1_17 |
Left |
9.99 |
0.36 |
0.06 |
0.51 |
1.57 |
|
s1_18 |
Right |
11.01 |
0.19 |
0.20 |
7.09 |
0.61 |
|
s1_19 |
Right |
18.15 |
0.23 |
0.28 |
Wide |
Over |
|
s1_20 |
Left |
4.12 |
0.33 |
0.21 |
0.05 |
2.25 |
|
s1_21 |
Left |
3.58 |
0.32 |
0.13 |
Wide |
Along Floor |
|
s1_22 |
Left |
9.39 |
0.33 |
0.18 |
1.49 |
1.85 |
|
s1_23 |
Left |
13.44 |
0.29 |
0.18 |
1.82 |
0.90 |
|
s1_24 |
Left |
2.96 |
0.31 |
0.23 |
4.28 |
2.31 |
|
s1_25 |
Right |
8.24 |
0.25 |
0.22 |
5.83 |
2.08 |

Table 2: Striker 2
|
Shot |
Foot Angle |
Launch Angle |
Distance Foot Away From Ball (BV) |
Distance Toe in Front of Ball (SV) |
Position of ball (m) |
|
|
(position) |
(°) |
(m) |
(m) |
x |
y |
|
|
s2_1 |
Right |
9.68 |
0.21 |
0.20 |
5.12 |
1.08 |
|
s2_2 |
Right |
13.08 |
0.24 |
0.22 |
5.52 |
0.52 |
|
s2_3 |
Left |
3.75 |
0.33 |
0.17 |
0.70 |
2.30 |
|
s2_8 |
Left |
14.22 |
0.38 |
-0.07 |
2.08 |
0.55 |
|
s2_9 |
Left |
11.43 |
0.43 |
0.15 |
0.93 |
1.00 |
|
s2_10 |
Middle |
17.06 |
0.40 |
0.21 |
6.86 |
Over |
|
s2_11 |
Middle |
21.24 |
0.33 |
0.07 |
– |
Over |
|
s2_12 |
Middle |
15.07 |
0.34 |
0.02 |
2.38 |
0.09 |
|
s2_13 |
Middle |
7.48 |
0.26 |
0.11 |
5.64 |
1.56 |
|
s2_14 |
Middle |
9.57 |
0.27 |
0.08 |
6.70 |
1.21 |
|
s2_15 |
Right |
5.90 |
0.22 |
0.09 |
5.13 |
1.98 |
|
s2_16 |
Left |
6.19 |
0.32 |
0.12 |
1.28 |
2.26 |
|
s2_17 |
Left |
13.69 |
0.38 |
0.01 |
1.52 |
0.55 |
|
s2_18 |
Left |
2.89 |
0.29 |
0.05 |
– |
Along Floor |
|
s2_19 |
Middle |
7.18 |
0.27 |
0.09 |
6.17 |
1.91 |
|
s2_20 |
Left |
7.72 |
0.31 |
0.09 |
5.82 |
1.51 |
|
s2_21 |
Right |
11.69 |
0.32 |
0.10 |
5.55 |
0.08 |
|
s2_22 |
Left |
12.13 |
0.39 |
-0.05 |
2.76 |
0.70 |
|
s2_23 |
Right |
1.76 |
0.20 |
0.04 |
5.79 |
2.23 |
|
s2_25 |
Middle |
3.91 |
0.36 |
0.00 |
5.34 |
2.27 |

Table 3: Striker 3
|
Shot |
Foot Angle |
Launch Angle |
Distance Foot Away From Ball (BV) |
Distance Toe in Front of Ball (SV) |
Position of ball (m) |
|
|
(position) |
(°) |
(m) |
(m) |
x |
y |
|
|
s3_1 |
Left |
3.65 |
0.42 |
0.15 |
0.94 |
2.34 |
|
s3_2 |
Right |
-1.47 |
0.24 |
0.18 |
6.78 |
2.28 |
|
s3_3 |
Left |
11.29 |
0.45 |
0.14 |
2.36 |
0.56 |
|
s3_5 |
Left |
10.64 |
0.36 |
0.13 |
1.35 |
1.62 |
|
s3_6 |
Right |
12.17 |
0.19 |
0.22 |
6.94 |
0.68 |
|
s3_7 |
Left |
8.88 |
0.38 |
0.19 |
0.69 |
1.92 |
|
s3_8 |
Left |
16.25 |
0.36 |
0.26 |
2.63 |
Hit Bar |
|
s3_10 |
Middle |
11.44 |
0.35 |
0.18 |
2.53 |
1.06 |
|
s3_11 |
Middle |
3.17 |
0.24 |
0.17 |
5.56 |
2.31 |
|
s3_12 |
Middle |
10.71 |
0.26 |
0.27 |
6.25 |
1.07 |
|
s3_13 |
Left |
8.12 |
0.40 |
0.12 |
0.36 |
2.00 |
|
s3_14 |
Left |
10.60 |
0.36 |
0.22 |
1.01 |
1.61 |
|
s3_15 |
Middle |
6.87 |
0.33 |
0.21 |
3.99 |
1.87 |
|
s3_16 |
Left |
15.02 |
0.33 |
0.21 |
1.42 |
0.60 |
|
s3_17 |
Right |
5.74 |
0.22 |
0.22 |
6.18 |
2.38 |
|
s3_19 |
Middle |
4.66 |
0.28 |
0.24 |
6.00 |
2.19 |
|
s3_20 |
Left |
6.23 |
0.40 |
0.09 |
0.13 |
2.21 |
|
s3_21 |
Right |
2.82 |
0.24 |
0.26 |
6.03 |
2.30 |
|
s3_22 |
Middle |
7.46 |
0.39 |
0.25 |
4.30 |
1.62 |
|
s3_23 |
Middle |
11.25 |
0.35 |
0.21 |
2.10 |
1.43 |
|
s3_24 |
Left |
10.35 |
0.44 |
-0.03 |
– |
– |
|
s3_25 |
Left |
11.94 |
0.37 |
0.25 |
3.92 |
0.79 |

Table 4: Striker 4
|
Shot |
Foot Angle |
Launch Angle |
Distance Foot Away From Ball (BV) |
Distance Toe in Front of Ball (SV) |
Position of ball (m) |
|
|
(position) |
(°) |
(m) |
(m) |
x |
y |
|
|
s4_1 |
Right |
2.17 |
0.20 |
0.15 |
6.67 |
2.07 |
|
s4_2 |
Middle |
7.02 |
0.30 |
-0.04 |
2.16 |
2.19 |
|
s4_3 |
Middle |
4.38 |
0.31 |
0.11 |
6.10 |
1.76 |
|
s4_4 |
Left |
3.47 |
0.41 |
0.07 |
0.69 |
2.29 |
|
s4_5 |
Right |
4.32 |
0.29 |
0.13 |
5.58 |
1.86 |
|
s4_6 |
Right |
3.97 |
0.23 |
0.04 |
5.94 |
2.16 |
|
s4_7 |
Middle |
7.56 |
0.37 |
0.11 |
2.86 |
1.46 |
|
s4_8 |
Middle |
2.58 |
0.29 |
0.20 |
5.73 |
2.21 |
|
s4_9 |
Left |
2.38 |
0.39 |
0.04 |
1.08 |
2.24 |
|
s4_10 |
Right |
1.18 |
0.26 |
0.13 |
5.95 |
2.30 |
|
s4_11 |
Middle |
14.93 |
0.26 |
0.01 |
2.81 |
0.61 |
|
s4_12 |
Middle |
9.82 |
0.25 |
0.20 |
5.92 |
0.72 |
|
s4_13 |
Middle |
9.27 |
0.26 |
0.01 |
2.40 |
1.84 |
|
s4_14 |
Right |
9.45 |
0.28 |
0.16 |
6.61 |
0.84 |
|
s4_15 |
Middle |
10.34 |
0.28 |
0.11 |
2.73 |
1.52 |
|
s4_16 |
Middle |
19.07 |
0.35 |
0.14 |
Wide |
Over |
|
s4_17 |
Right |
9.94 |
0.24 |
0.03 |
6.06 |
1.24 |
|
s4_18 |
Right |
0.76 |
0.18 |
0.13 |
6.13 |
2.31 |
|
s4_19 |
Left |
7.32 |
0.34 |
0.10 |
2.34 |
1.80 |
|
s4_20 |
Middle |
10.68 |
0.26 |
0.18 |
5.93 |
0.60 |
|
s4_21 |
Right |
3.34 |
0.26 |
0.06 |
5.14 |
2.10 |
|
s4_22 |
Middle |
9.52 |
0.33 |
0.09 |
3.14 |
1.06 |
|
s4_23 |
Right |
2.75 |
0.28 |
0.27 |
5.81 |
2.25 |
|
s4_24 |
Left |
16.55 |
0.40 |
0.09 |
3.03 |
Over |
|
s4_25 |
Right |
11.53 |
0.24 |
0.18 |
7.01 |
0.71 |
Correlations
Below are the summaries of the analysis that took place and the variables which were correlated. As a large sample size was present in this study, normality was assumed, and thus the Pearson’s correlation coefficient calculations were used.
1) Foot angle (left, middle or right) against where the ball crosses the goal line in terms of the x position
Initially, the position of the foot appeared to have some determination to where the ball ended up crossing the line. As an initial investigation, the goal was split into sections horizontally, each of equal width (2.44 m), being classified as either the left, middle, or right of the goal. The results were then tabulated as below.
Table 5
| Ball Position |
Ratio |
% |
|||
| When foot pointing left = | LEFT |
22/28 |
79 |
||
|
(<-5°) |
MIDDLE |
5/28 |
18 |
||
| RIGHT |
1/28 |
4 |
|||
| Ball Position |
Ratio |
% |
||||
| When foot pointing forwards = | LEFT |
7/27 |
26 |
|||
|
(-5°<0>5°) |
MIDDLE |
7/27 |
26 |
|||
| RIGHT |
13/27 |
48 |
||||
| Ball Position |
Ratio |
% |
|||
| When foot pointing right= | LEFT |
1/27 |
4 |
||
|
(>5°) |
MIDDLE |
0/27 |
0 |
||
| RIGHT |
26/27 |
96 |
|||
It can be seen from the above table that there appeared to be some link between which direction the foot is pointing, and where the ball ends up. It is important to note that the strikers were specifically asked to put the ball down the sides, not down the centre of the goal. Therefore the two examples of where the foot pointed the opposite way to where the ball ended up may well have been a miss hit of the penalty. Similarly, when the ball went down the centre of the goal, as this was not intended, it may have been due to a poor strike.
Below is a diagrammatic depiction of these findings. (Figure 12)

Following on from the initial statistical analysis, further investigation looked into the correlation between foot position and ball position.
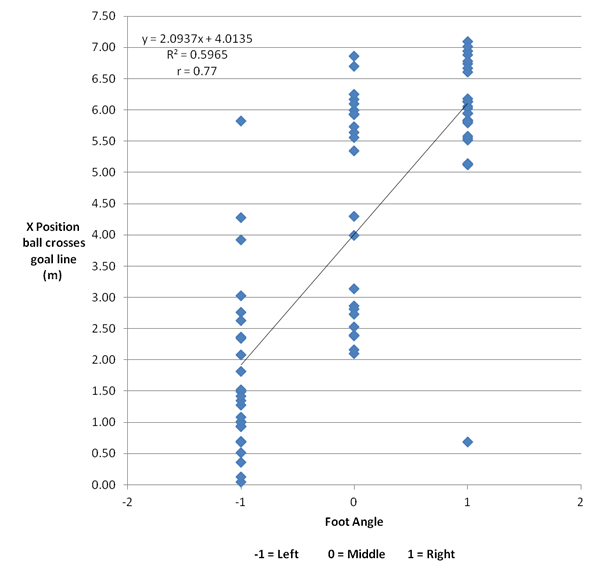
First, a simple scatter plot was constructed (as shown above), using the x distance of where the ball crosses the line (measured from the top left hand corner) rather than sectioning the goal into left, middle or right. From a linear line of best fit, this gave a correlation coefficient of 0.77; this is a very strong correlation. Additionally a Kendall Tau correlation was completed, which yielded a correlation coefficient of 0.609, significant to p=0.01. Again this confirms a very strong, significant correlation between the two.
To further quantify this numerically, linear regression was completed based on the following principles:
Equation of a line: y=mx + c
y = x position ball crosses line
m = the coefficient
x = Foot angle (-1, 0 or 1 for Left, Middle or Right respectively)
c = y interceptIf, as we expect, the foot angle affects the final position of the ball in the goal, and hence the direction of the penalty, then we would fine c to be roughly equal to 3.66 m (the middle of the goal), and the m value to be significantly different from 0. This would mean that if the foot was pointing left, (x=-1, c ≈ 3.66), then the m value would shift the y value (position of the ball in the goal) into the expected direction. The results found were as follows:
y = 2.09x + 4.01
p = 3.09 x 10-16
Confidence intervals: Lower 95% = 1.69, Upper 95% = 2.49
This confirms our initial thought that the plant foot position can be used to predict which side of the goal the ball will end up. The p value is very significant, and the values of the confidence intervals both fall in a range which confirms this correlation.
2) Distance foot away from ball against where the ball crosses the goal line in terms of the x position
As the distance the toe was away from the ball was also taken from the video footage, a correlation between this and the position of the ball when it crossed the line was also calculated. This was done using a Pearson correlation which gave the following result:
r = -0.713
p = 0.000 (3dp), significant to the 0.01 level
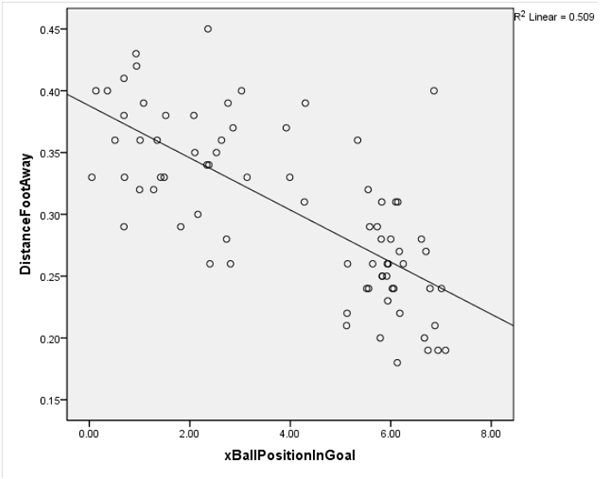
This shows a very strong correlation between the two variables, and also that this correlation was highly significant. This means that another determinant of where the ball crosses the goal line (horizontally) can be predicted from how far the toe of the plant foot is away from the centre of the ball. However, it is important to note that this measurement of distance was taken from the toe of the plant foot, and so when the foot was angled to the left, this would increase the distance the toe was from the centre of the ball, and so there may be some overlap between this finding and the above correlation of foot position.
3) Distance foot in front of ball against where the ball crosses the goal line in terms of the y position
This next analysis was used to see if there was any correlation between the positioning of the plant foot forward / backward in relation to the centre of the ball, and the height that this ball finished up in the goal. (I.e. if your plant foot landed behind the ball there would be a greater chance that the penalty would end up near / over the crossbar.) As before, a Pearson Correlation was carried out, giving the following results:
r = -0.072
p = 0.549
These results would appear to suggest that although the correlation found was not significant, there is no correlation between plant foot position in terms of in front / behind the ball and the vertical position of the ball as it crosses the line.
Two examples which appear to confirm this lack of correlation are as shown:
Shot s3_6
Distance toe in front of ball = 0.22 m
Height above the ground the ball crosses the goal line = 1.76 mShot s3_17
Distance toe in front of ball = 0.22 m
Height above the ground the ball crosses the goal line = 0.06 mThis shows the even with the same plant foot distance from the ball, there is a large deviation between the height at which the ball crosses the line.
4) Distance foot in front of ball against foot angle (left, middle or right)
Finally it was investigated whether there was any correlation between the positioning of the foot in terms of its angle, and its position in front / behind the centre of the ball. Again, a Pearson Correlation was applied to give the following results:
r = 0.226
p = 0.041, significant at the 0.05 level
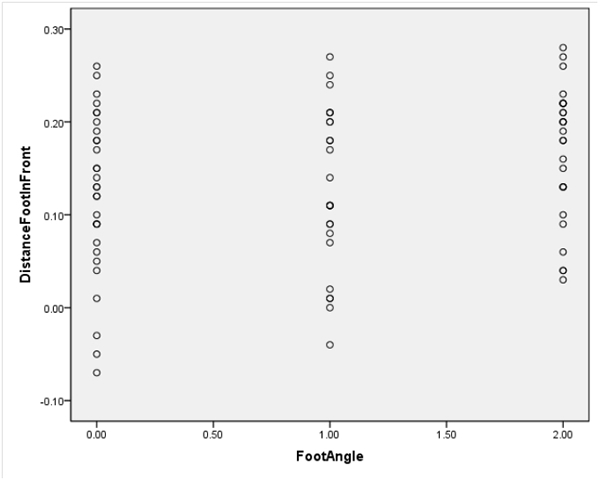
These results show only a weak correlation, although significant, between the two plant foot variables. However, subjectively inspecting the graph, it can be seen a slight tendency to have the plant foot behind the ball when the foot is pointed left (and vice-versa), and to have the plant foot further forward when it is angled right. Therefore there may be some correlation between the forward / back placement of the plant foot and where the penalty ends up in the goal if the correlation between foot angle and x position in the goal is anything to go by. This would need further analysis.
Discussion and Conclusion
The position of the plant foot in terms of which way it is pointing in respect to the goal appears to be a predictor of where (horizontally) the penalty will end up (be it in the left hand side of the goal as you look at it (keepers right), the middle or the right hand side). Therefore, it may be of use to goal keepers to look closely at the angle of this plant foot in order to predict the direction of the shot as this report finds there is a strong correlation between the two. 77% of the time, they will be able to predict correctly. In terms of the ball going down the middle, we cannot really make any clear conclusions on what the foot pointing forwards means. As the strikers used in this case study were asked to aim in the outer sections of the goal, strikes down the middle are likely to represent ‘miss-hits’, and so further analysis would be required to validate this.
In the light of these findings, we feel it necessary to relate them as much as possible back to the importance in a practical sense, and thus some investigation into time was carried out. This was to identify that even if the goalkeeper could predict from the foot placement where the shot would end up, could this actually give them enough extra time to save it?
Firstly it was calculated how long, if the goalkeeper only reacted to the initial movement of the ball (i.e. no prediction), before the shot crossed the goal line. This was done for three typical ball speeds: 25ms-1, 20 ms-1 and 15 ms-1 using Pythagoras (Figure 13) and Time = Distance / Speed.
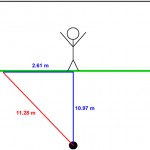
N.B. 2.61 m was chosen as this marks the 1 m area which the strikers were aiming for:
Using the Pythagoras distance calculated at 11.28 m, the times taken for the ball to cross the goal line were as follows:
25 ms-1 = 0.451 seconds
20 ms-1 = 0.564 seconds
15 ms-1 = 0.752 secondsFive shots were chosen at random, and the time between the instance at which the whole foot was planted, and the first frame of ball movement was noted and averaged to give a value for the additional time a goalkeeper could acquire if they looked at the plant foot. The value was calculated as 0.078 seconds. To make this value more meaningful, it was calculated in relation to the total time it took the ball to cross the line.
Ball travelling at 25 ms-1 = 17.3% additional time
Ball travelling at 20 ms-1 = 13.8% additional time
Ball travelling at 15 ms-1 = 10.4% additional timeTherefore although only rough calculations used as an example (not taking into account other variables such as the velocity of the goalkeeper’s centre of mass), it can be seen that looking for these visual cues before ball contact (if they can be proven to be good predictors) can give the goalkeeper an advantage, and for any sporting performance this is sought after. The faster they can judge which direction the penalty is going, the greater the chance they have of initiating a dive in enough time to intercept the ball before it crosses the line. However it is important to note that there is a trade-off in successful goalkeeping between initiating late movements that may not offer sufficient time to intercept the shot, and early movements that force goalkeepers to rely on anticipating kick direction (Dicks et al., 2010). Additionally, if the keeper moves before the ball is struck, some players make use of a ‘closed loop’ strategy, where the striker tries to take into account the goalkeeper’s actions, so as to place the ball to the opposite side of the goal (Kuhn, 1988). Therefore the keeper must decide when to dive, even if they can make use of visual cues. Too early allows a closed loop striking strategy, too late may not leave enough time to intercept the ball (Moyra et al., 2003).